Md Shahriyar Al Mustakim Mitul's Blog

Artificial Intelligence : Reinforcement Learning- Q Learning (Part 35)

Md Shahriyar Al Mustakim Mitul's photo
Md Shahriyar Al Mustakim Mitul
·

15 min read

Why AI and why now?

Basically this is Moore's law and shows how computational powers are going to increase over the years. It was a prediction and we have already gone beyond

And we've already surpassed the brain of an insect for an average computer that you can buy for 1,000 bucks. We're sitting at about the processing power of the brain of a rat. By 2025, we'll be at the brain of a human.

So in 1997, DeepMind was the first compute to beat Garry Kasparov in chess. It was a huge thing.

Now on any phone, you can install an app with chess, which no human player will ever beat because computers are that good now.

And then just recently in March 2016, a computer won against the 18 world times champion, 18 world champion of the game of Go, Lee Sedol.

You'll see that we're using games to train AI. Why are we doing that?

Because games are a confined environment where if we can beat a game, using an artificial intelligence, then we can use the same principles to apply it to business, and that's the exact same thing that the team at Google DeepMind who created AlphaGo who won against Lee Sedol

They applied artificial intelligence to a Google warehouse to control the air cooling

and what they found this is the electricity bill, the electricity consumption.

You can see it's going like this (Left black lines) As soon they switch on the AI, bam, it goes down. (Red line) And then they switch it back off, it goes up. (black lines on right). They were able to save 40% on their electricity bill.

Check out this blog

Reinforcement Learning

The thing is we already know how we, humans, learn. We understand the concepts of intrinsic and extrinsic rewards that guide us to become better at things.

For example, if you're playing bowling - you know that you need to hit the pins and a strike is a perfect shot.

We know this because we are rewarded with points for hitting the pins down and we are "punished" with no points when your ball ends in the ditch.

So your brain projects those conditions of the environment onto your actions and that's how you know when you are doing good and when - not so much. And that's how we learn.

But how do we explain that to an AI? Let's learn Q-Learning to describe the process

Q Learning

Assume that this is an environment and we have sent an agent to to get to the white ring within the environment

So, what it will get is state of the environments and rewards and depending on that, it will take actions.

So, what is a state?

It basically means a situation.Assume that the agent started entering from this place

So, it will see that on left and right , it has space to move and get reward 1 to mean, that you are okay to move. then may be it may choose left

Still there is space to move on right as left side is blocked and no space out there.

So, now it can move to right .

Now it will see that, although there are space to move right and left but one it moves , it will end up getting a blocked road (follow the yellow lines)

So, now the reward point should be -1 to mean, don't go that way and get back.

This was just an example to make sure, how state and reward influences our agent's action.

The Bellman Equation

So, here for this concept , we will have state, action and reward alongside discount. We have learned about state, action and reward earlier. We will know about discount later.

So, let's start a case

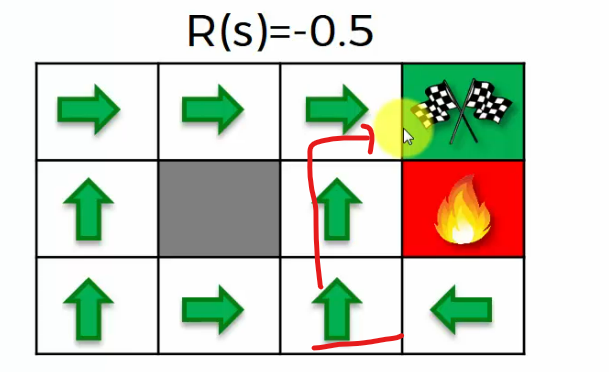
here the red box means we should not go there and is fire. The green box is our desired place.

So, we can set that by reward -1 and +1

So, how can it reach there? Taking actions , right?
Assuming the agent can go to right, left, up, down (only if the road is not blocked)

So, it can go up and up

It can come back and go right and right

Now, let's backtrack and understand how can we reach the green box.

We know green box is our desired one, and if we are just before that green box, doesn't that mean that, by taking 1 step( to right), we will get our reward +1?

Yes ! So, we can set Value = +1 there to mean that, if we somehow (by going right, left, up, down) reach here, we we have no restriction or blockage and can go to the green box.

Now, how can we event reach at this white box?

We have to be here to go to that previous box, right?

So, again. If we reach here, doesn't we have have space at right to go to the green box?

Yes! So, we can assign Value +1 here too. Just to mean, somehow reach here, and you will get good success in future. Just like how our parents mention" Just pass SSC and you don't need to study" And once we pass the HSC, they say "Just Pass the HSC and you don't need to study" and this is a trap 😒

then again, how did we reach that box?

Surely from here and again from this point, we can reach the Green box.

So, we can set the value +1 here as well

And we repeat this again and again, and reach the start

So, we can set this values for these white boxes.

Now, what about after setting these values, our agent starts from this point?

Now, it still has the values and the problem arises where to move. (Note: You may ask that, we can change the value and repeat the process . Why should we have the values V=1 for boxes below the agent's current position. Okay! So, those were created previously and we have to keep in mind, we are solving the problem in a way. So, our way was to firstly generate some value , V. We have done that till start and then the agent changed it's starting point. It's not what we thought previously before going for our way of solution)

And that's why we will cancel this approach

So, to solve this issue, we will use Bellman equation

V is value of being in a current state, S is the current state , S prime is the following/next state. But to go to different state, we need actions.

But what action should we take?

Shouldn't we take the action that gives us maximum reward?

For that we have R(s,a) which returns a reward after taking an action to reach a state.

But we need the max value, so Max(R(s,a)). For every one of the possible four actions, we're going to have a equation like this.

So, let's apply this in this :

For every state, we will have a different equation.

Now, starting from the white box (We have previously mentioned why we started from that position)

Now, what's the equation for this box? here max(R(s,a)) will return +1

Why?

So, let's see what possible states and actions it can take from here. It's currently in state 2,2 ( assuming it as a matrix)
So, R((2,2), Right), R((2,2), Left), R((2,2), Down)

R((2,2), Right) will give us +1 as we have got our goal. Others won't be able to give us +1 rather smaller amount.

So, Max(R((2,2), Right), R((2,2), Left), R((2,2), Down)) gives us +1.

Also, now, as we have decided that, we will move to right, on the right, the gamma value is 0 as it's the goal state.

V(2,2)=Max((2,2),Right)+0*V(2,3)=1+0

So, V(2,2) will have the value +1

Next if we backtrack, we may come from this white box. Let's see what's the value for this box

Here for this state, we can go to right , left, down

Wherever we go, we will get value 0. Why, because we don't have our goal in right, left or down.

V(1,2)=Max((1,2),Right) + Gamma*V(2,2)=0+Gamma*V(2,2)

If we set gamma to =0.9

So, V(1,2)=0.9*(V(2,2))= 0.9*1 = 0.9

V(0,2)=Max(R(0,2),Right)+0.9*V(1,2)=0(as we can't get goal state in right)+0.9*0.9= 0.81

So, we repeat this process and get this finally

Now, we will start to have value from this

As from this point we can easily move to Up (the upper box has V=1)

On the left , we have a wall (Blocked)

So, we will go Up and the equation will be

V(2,1)=Max((R(2,1),Up),(R(2,1),Right),(R(2,1),Down)) +0.9*V(Next state)

Let's go to Up (2,2)

V(2,1)=Max(R(2,1),Up)+0.9*V(2,2) = 0+0.9*1=0.9

In this way, we back track and get this

And finally, we complete all of the White boxes with this

Now, here we know we have got value for each boxes but also, from each box, we have decided a state to move. Didn't we?

These are the new action we are planning to take and move to new state.

Markov Decision Process (MDP)

Before learning about MDP, let's learn Deterministic search

If we say, go up, it will go up

And Non Deterministic search says, if we say to go up, it might go up (80% chances), it might go left or, right

So something that is out of the control of the agent, something that it cannot predict, that's what we are modeling here in non-deterministic search.

And this is where we have directly approached two new process

Markov Process-> So a Markov property is when your future states, so not just your choice, but the whole thing, your choice and the environment, it will only, like, the results of the action you take in that environment will only depend on where you are now, it will not depend on how you got there.

For example,

Here we may appear in this stage from wherever we want. It does not even matter, how we reached at that position (2,1)

So, the probability to go to left, right and up will be same (As we are not bothered about our past paths, we are just thinking about present)

Markov Decision Process (MDP)->

So a Markov decision process is exactly what we've been discussing up 'til now. So that the agent lives in this environment where it has control. But now it has a little bit less control.

It can decide to go up, but it actually knows, "Okay, so if I go up, there's an 80% chance, there's a 10% chance on the left, 10% chance I'll go right."

So not everything is fully under its control.

We have previously learned about Bellman equation.

Now because we have some randomness in our whole process, this part will change because we don't actually know which state we'll end up in, we don't know what S prime will be. Will it be, if we're going up, will it be up or will be left, or will be right?

So here, we're going to replace this (S prime), so there's three possible states we can end up in.

Now, we will multiply with the chances we had (80% changes to move up, 1 0% chance to move left, 10% to move right) and sum that.

then we get this equation

This part is exactly what we did earlier. Adding those three states.

Policy Vs Plan

So previously we're dealing with we've deterministic search (We fixed a path to move and then moved)

And this was our plan to move towards the goal

But we actually can't move wherever we want. Due to environment and challenges, we generally have to deal with Non-Deterministic search.

So, now the values do change

How? Why has they changed

Talking about this box, we previously had V=1 but now 0.86

Now, this is the direction (Things might make sense at first , specially for (2,1) and (3,0))

Let's talk about (2,1) state which seems weird as it should have gone up or down.

Well, 80% of the time it'll bump back into the wall and stay in this state but 10% of the time it'll go here and 10% of the time it'll go here.

So it rather bounces into the wall a couple of times and then it will go either right or left at some point because that randomness is gonna happen.

Again it's same for the (3,0) state. At some point it will move to the left.

So, this is the plan now:

Living Penalty

We can add a reward of -0.04 ( a penalty)

Our agent gets this reward when he enters a box. So whenever he promises an action, he goes here then he will get this reward minus 0.04.

Why are we adding this?

The longer he walks around, the more he accumulates this negative reward, and therefore it is an incentive for him to finish the game earlier as quickly as possible.

Let's understand this by an example:

--> For Penalty 0

We get the same plan we had. There will be no change.

--> But for Penalty 0.04,

Things did change for this two states. Now you can see they are exactly in the same direction , they should have been. Why?

Because if they now follow the previous plan ,

they will remain in that stage for 80% of the time and the penalty will get added to the value. (Penalty is added every single time , one move to a new box or the same box, so the less box one travels, the better for the agent)

Our goal is to have max value and to avoid the penalty, it will move to another direction now.

--> Now, if the penalty is 0.05

this will change for state (2,0) because according to previous plan, the agent would travel to this path

So, it would need to cross 6 box (tile) before going to goal box.That would add a lots of penalty to the value.

But if the direction changes, the agent can go to desired state earlier

--> But for penalty 2.0

It's so high that the agent just wants to get out of the game in any way possible, even if it's just by jumping into the fire pit. He will do it.

So, we can't have whatever penalty we want to add. If we add a big number of penalty, we might not even be able to reach our goal tile.

Now, let's proceed towards Q learning.

So, in Markov Process, the agent reached in the box somehow. We are not bothered about it. Now it will try to look for the best possible state it can go

Let's now replace V with the value of each state with Q

So Q here represents, rather than the value of the state, it represents, let's go with quality.

From the image you can see , when we go to upper state from the S zero state, we have a value Q(S zero, Action 1) and in the same way, we had all other values when we take other actions to move to other tiles/boxes.

Let's see the difference between V(S) and Q(S,a)

V(s) means value of a state

and we know how to get the value :

And Q(S,a) which means Quality of action .

Here it means We are in (1,0) position but we want to go to upper box with action a.

So what we're saying here is that, okay, so by performing an action,

you're going to get a reward R(s,a), plus, which is a quantified metric,

plus you're gonna get, end up in a state, we don't know which one.

It could be here, it could be here, it could be here.

But here is the expected value of the state that you're going to end up in. And now we're going to multiply it by discounting factor(gamma) because that is one move away. So that is our Q-value for this performance section.

But, it shows that, V(S) = Max(Q(s,a))

We replace this value then, as V(S) = Q(S,a)

Temporal Difference

In the Non-deterministic way (due to environment and others, our agent might not go where we wanted), we have this

But in the deterministic way, we are sure that our agent takes the action we mentioned. So, no need to add summation of other chances.

Now, let's see an example

Assume that this is where our agent is currently. And he is thinking of going up and so, he has got a value Q(s,a) in the cell.

Now, he has moved to the upper cell.

So, we have a value in the cell which is R(s,a)+gamma*max(Q(s prime, a prime))

From these, we got temporal difference (TD)

How do we use this? And why is it called a temporal difference?

Well, the reason it's called a temporal difference is because you're basically calculating the same thing. Both are some way of representing Q(s,a) but but the difference is time.

The last part is the Q(s,a) we had earlier and the first part is the one we have once we moved to new cell.

We don't want to completely change our Q-values. We want to, like, change them step by step, a little bit by little bit. And that's why we're going to use this temporal difference in a specific way.

We are going to update our Q(s,a) and here alpha is our learning rate.

Let's include time now:

So, our current Q is going to be equal to our previous Q plus whatever temporal difference we found times alpha.

and we can write this:

Done!!

Reading Materials

temporal differenceMarkov decision ProcessBellman equationQ-learning